How Deep Can You Measure?
Depth of measurement varies based on two properties: the energy of the element and the density of the matrix. As each photon is emitted as a K or L shell line, the spectral peaks resulting from such fluorescence can be thought of as atom counts of sorts - though the quantity of photons is determined by both the voltage of the tube and the depth of penetration. The depth of penetration can be calculated by the following equation:
I/I0 = e[-(μ/ρ)x] (1)
where I is the quantity of photons returning from the sample, I0 is the quantity of photons entering the sample, μ/ρ represents the mass attenuation coefficient of a given element for a particular matrix, and x represents the density of the object. You can find mass attenuation coefficients at NIST.gov. Assuming a limit of 1% returning photons from a silicate matrix, the depths of analysis can be approximated by the following formula:
d(cm) = 4.36/(-μ/ρ)ρ (2)
where d(cm) is the depth in centimeters. Thus, you only need two variables to calculate the depth of a given photon’s energy in a given matrix. You can obtain mass attenuation coefficients (-μ/ρ) from the NIST website. Just click the link, put in the chemical formula, select ‘Mass Attenuation Coefficient (cm2/g) vs E (keV) Graph’ as the Type of Data, and choose an appropriate energy range Sub-Range - I usually just do 1 - 40 keV but you can choose whatever range you like. You will then receive the mass attenuation coefficients in a small table to the lower right of the page. Then you need a density estimate for the sample. For water this would be 1 g-cm-3, for a silicate it would be 2.648 g-cm-3. Copy these data and use equation (2) to obtain a list of estimated measurement depth for each element:
Depth of measurement varies based on two properties: the energy of the element and the density of the matrix. As each photon is emitted as a K or L shell line, the spectral peaks resulting from such fluorescence can be thought of as atom counts of sorts - though the quantity of photons is determined by both the voltage of the tube and the depth of penetration. The depth of penetration can be calculated by the following equation:
I/I0 = e[-(μ/ρ)x] (1)
where I is the quantity of photons returning from the sample, I0 is the quantity of photons entering the sample, μ/ρ represents the mass attenuation coefficient of a given element for a particular matrix, and x represents the density of the object. You can find mass attenuation coefficients at NIST.gov. Assuming a limit of 1% returning photons from a silicate matrix, the depths of analysis can be approximated by the following formula:
d(cm) = 4.36/(-μ/ρ)ρ (2)
where d(cm) is the depth in centimeters. Thus, you only need two variables to calculate the depth of a given photon’s energy in a given matrix. You can obtain mass attenuation coefficients (-μ/ρ) from the NIST website. Just click the link, put in the chemical formula, select ‘Mass Attenuation Coefficient (cm2/g) vs E (keV) Graph’ as the Type of Data, and choose an appropriate energy range Sub-Range - I usually just do 1 - 40 keV but you can choose whatever range you like. You will then receive the mass attenuation coefficients in a small table to the lower right of the page. Then you need a density estimate for the sample. For water this would be 1 g-cm-3, for a silicate it would be 2.648 g-cm-3. Copy these data and use equation (2) to obtain a list of estimated measurement depth for each element:
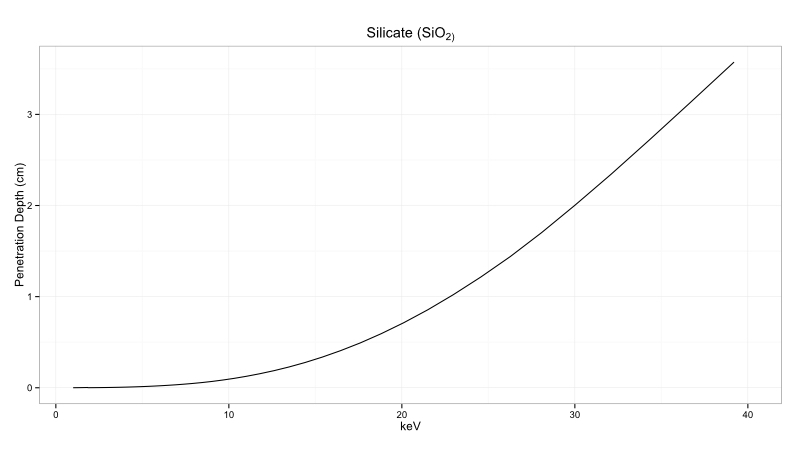
Figure 1: Depth of measurement in a pure silicate
Elements that fluoresce with low energy, such as silica at 1.7 keV, will only return photons from 20 μm deep into a SiO2 matrix, while elements that fluoresce at higher energies, such as Zirconium at 15.77 keV, will return photons from as deep as 3.4 mm. As a consequence, elements with higher energies of fluorescence will be more easily identified in smaller concentrations. As energy in x ray tubes is non evenly distributed, there is a further discrimination against the fluorescence of elements on the extreme ends of an energy spectrum (near 1 and 40 keV). Furthermore, the fluorescence of one element can influence that of another. A high concentration of Zinc, with a K-alpha fluorescence of 8.78 keV, sits on the absorption edge of Copper, with a K-alpha fluorescence of 8.01 keV. A high concentration of Zinc will distort the quantity of Copper present in the spectra.
It may be more intuitive to think about this in terms of a table:
Elements that fluoresce with low energy, such as silica at 1.7 keV, will only return photons from 20 μm deep into a SiO2 matrix, while elements that fluoresce at higher energies, such as Zirconium at 15.77 keV, will return photons from as deep as 3.4 mm. As a consequence, elements with higher energies of fluorescence will be more easily identified in smaller concentrations. As energy in x ray tubes is non evenly distributed, there is a further discrimination against the fluorescence of elements on the extreme ends of an energy spectrum (near 1 and 40 keV). Furthermore, the fluorescence of one element can influence that of another. A high concentration of Zinc, with a K-alpha fluorescence of 8.78 keV, sits on the absorption edge of Copper, with a K-alpha fluorescence of 8.01 keV. A high concentration of Zinc will distort the quantity of Copper present in the spectra.
It may be more intuitive to think about this in terms of a table:
| Element | Emission Line | Energy (keV) | Depth (μm) |
|---|---|---|---|
| O | Kα1 | 0.53 | 0.01 |
| Na | Kα1 | 1.04 | 7 |
| Mg | Kα1 | 1.2 | 9.6 |
| Al | Kα1 | 1.47 | 17 |
| Si | Kα1 | 1.74 | 27 |
| P | Kα1 | 2.01 | 13 |
| Ca | Kα1 | 3.69 | 64 |
| Cr | Kα1 | 5.41 | 192 |
| Fe | Kα1 | 6.40 | 300 |
| Cu | Kα1 | 8.01 | 580 |
| Zn | Kα1 | 8.64 | 770 |
| Pb | Lα1 | 10.55 | 1,130 |
| Zr | Kα1 | 15.78 | 3,840 |
Table 1: Depth of select elements in a silicate
However, density is important too. The same physical relationship is present between elements in a denser matrix, however the total depth is considerably shorter:
However, density is important too. The same physical relationship is present between elements in a denser matrix, however the total depth is considerably shorter:
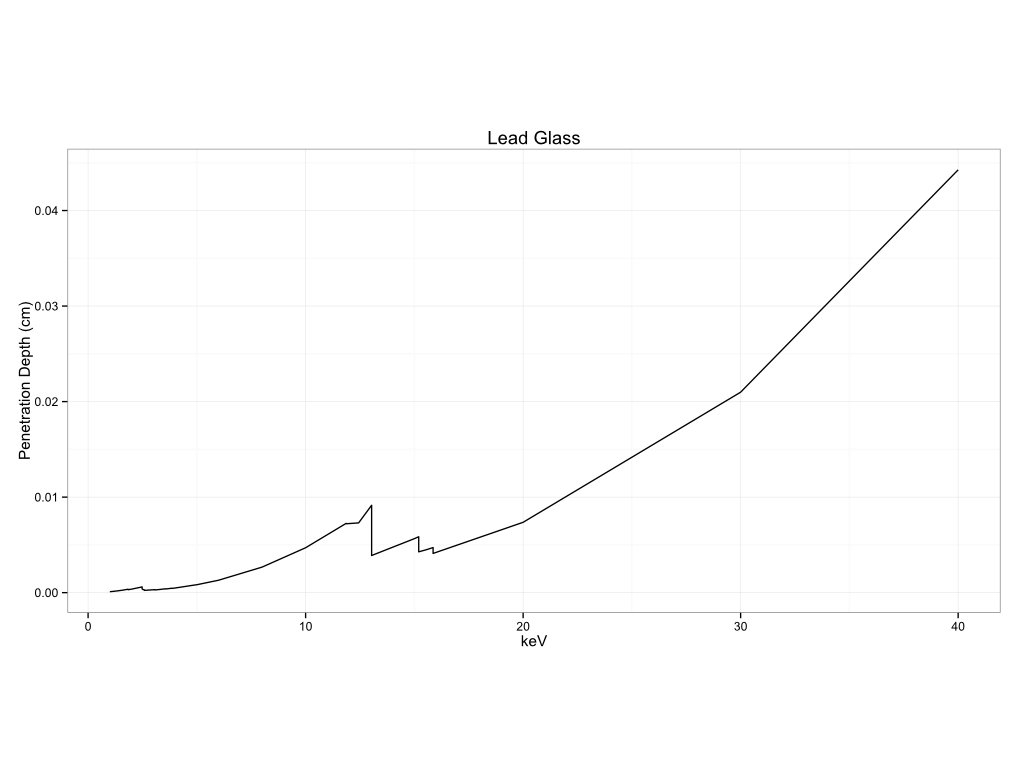
Figure 2: Depth of measurement in a lead glass.
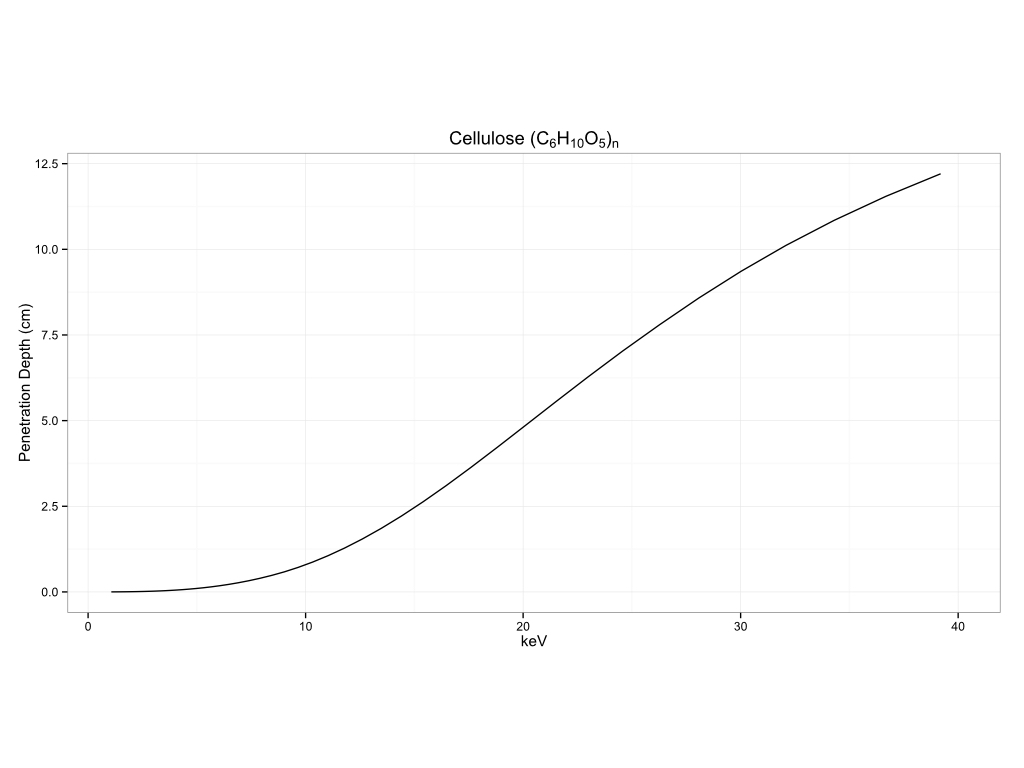
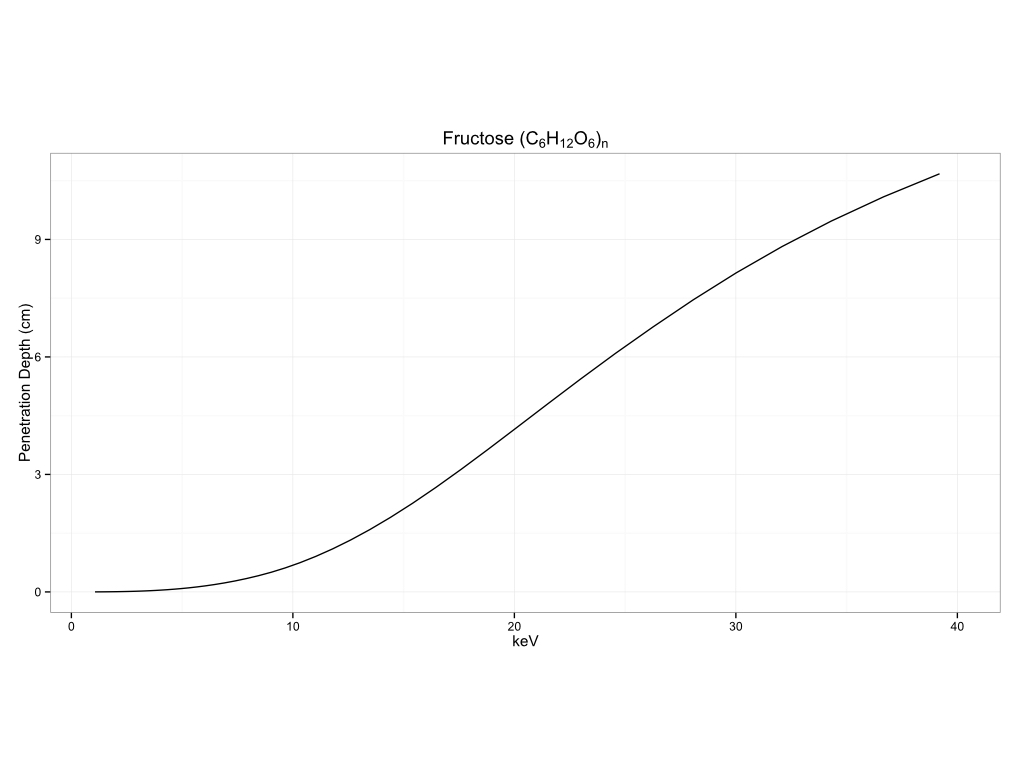
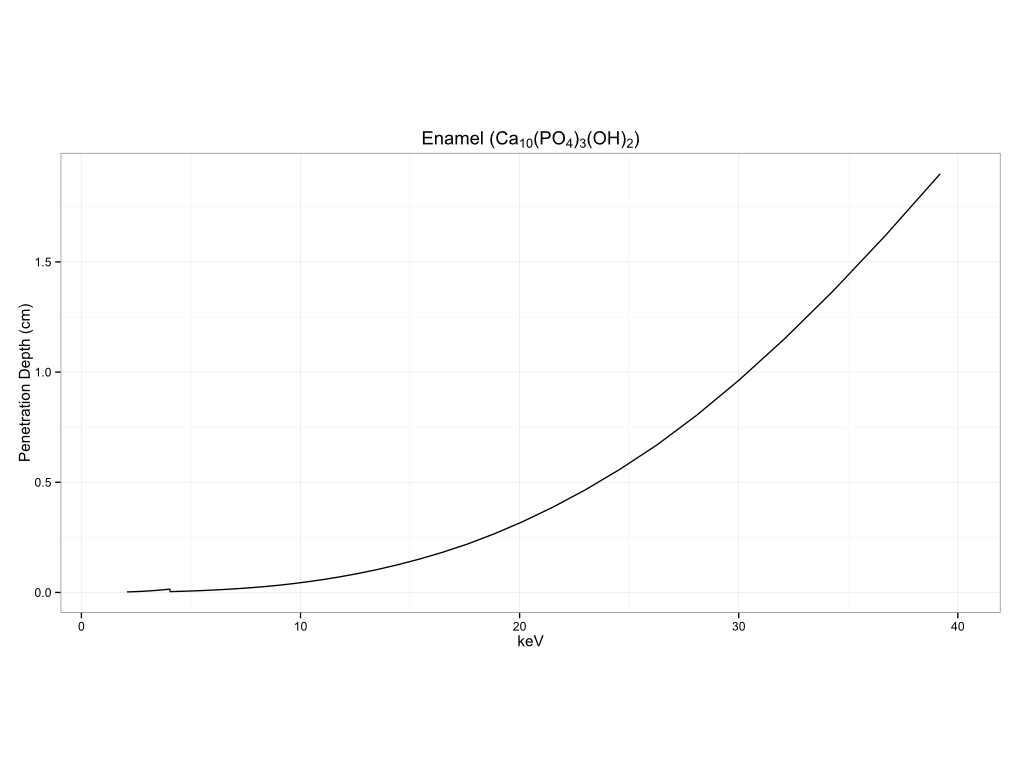
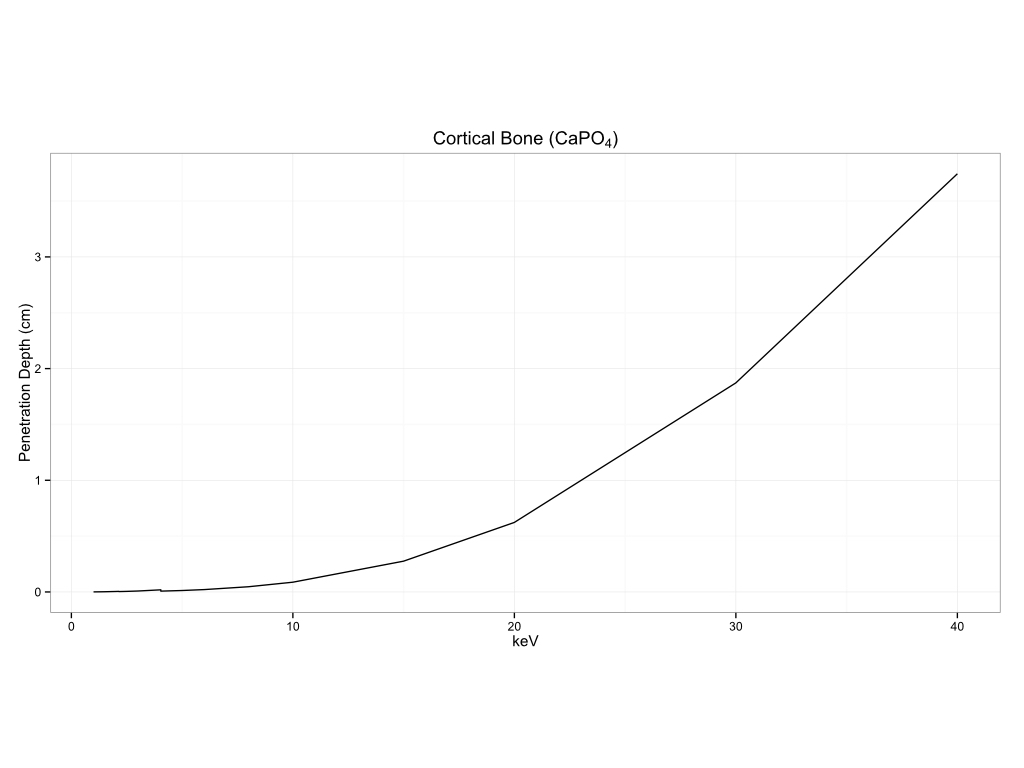
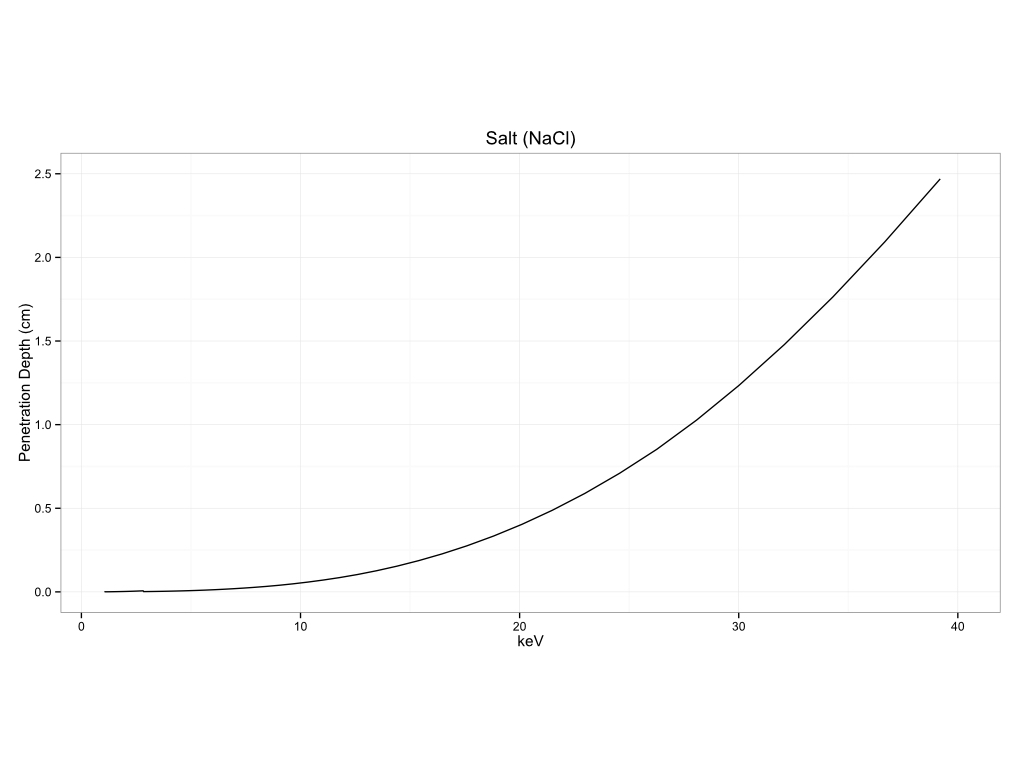
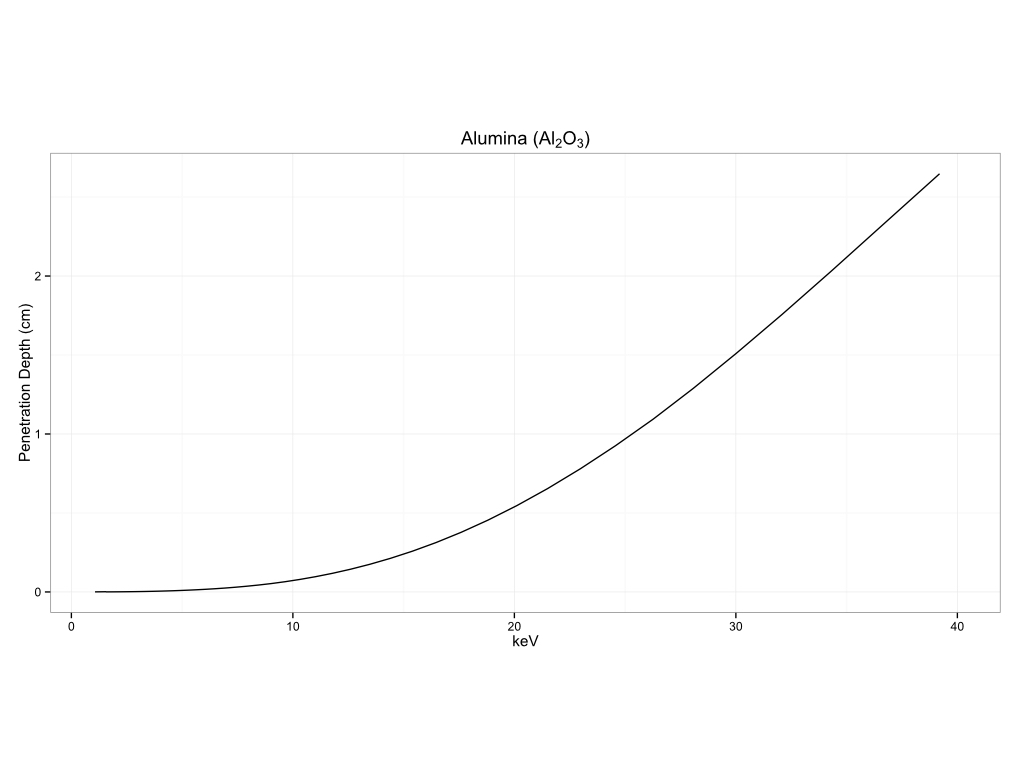
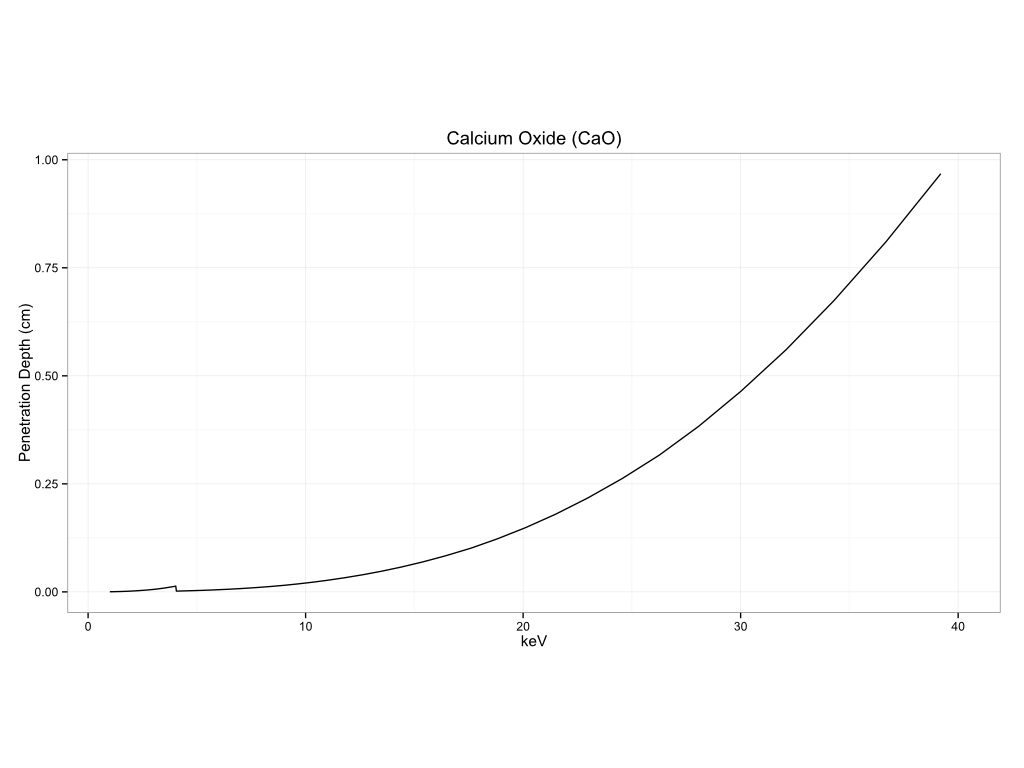
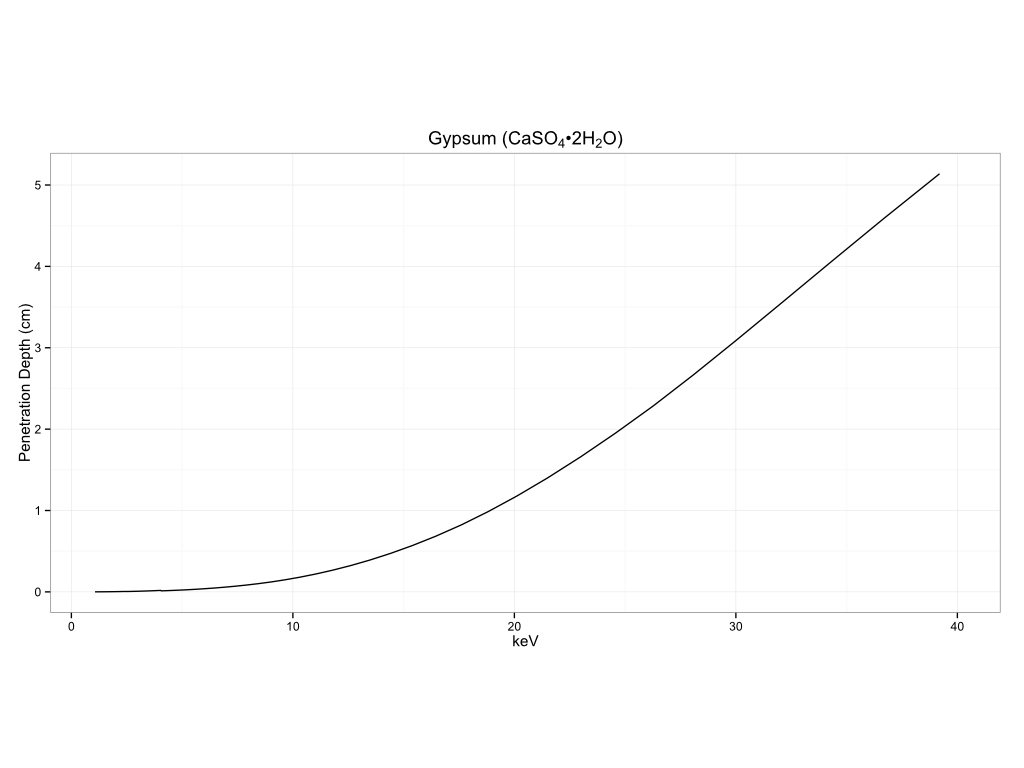
You can see how this can vary by matrix to matrix. I am including a number of examples of measurement depth in different matrices below. The first section will be for common substrates, biological materials, historical pigments, metals, and plastics.
You can see how this can vary by matrix to matrix. I am including a number of examples of measurement depth in different matrices below. The first section will be for common substrates, biological materials, historical pigments, metals, and plastics.
Common Substrates
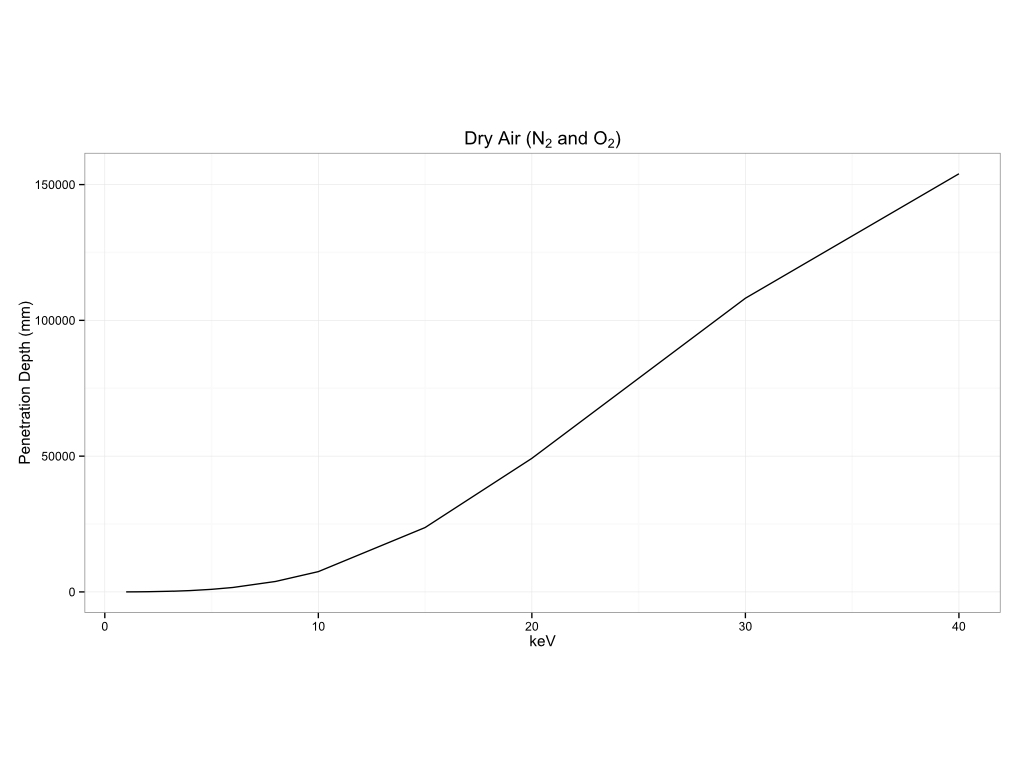
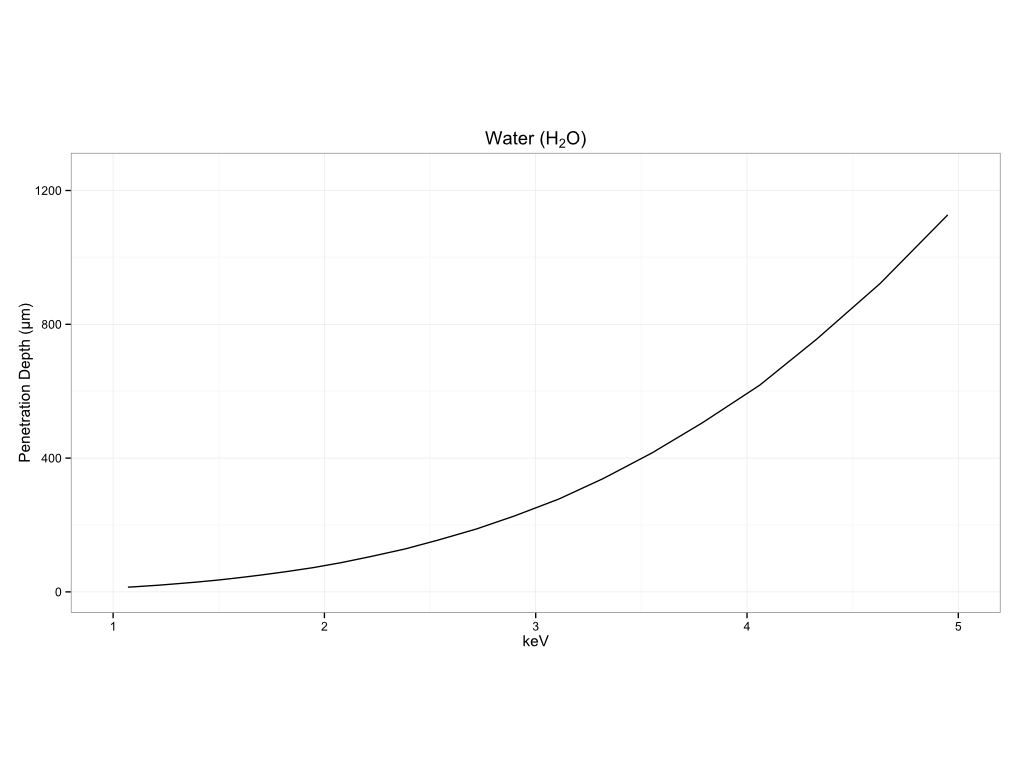
Metals
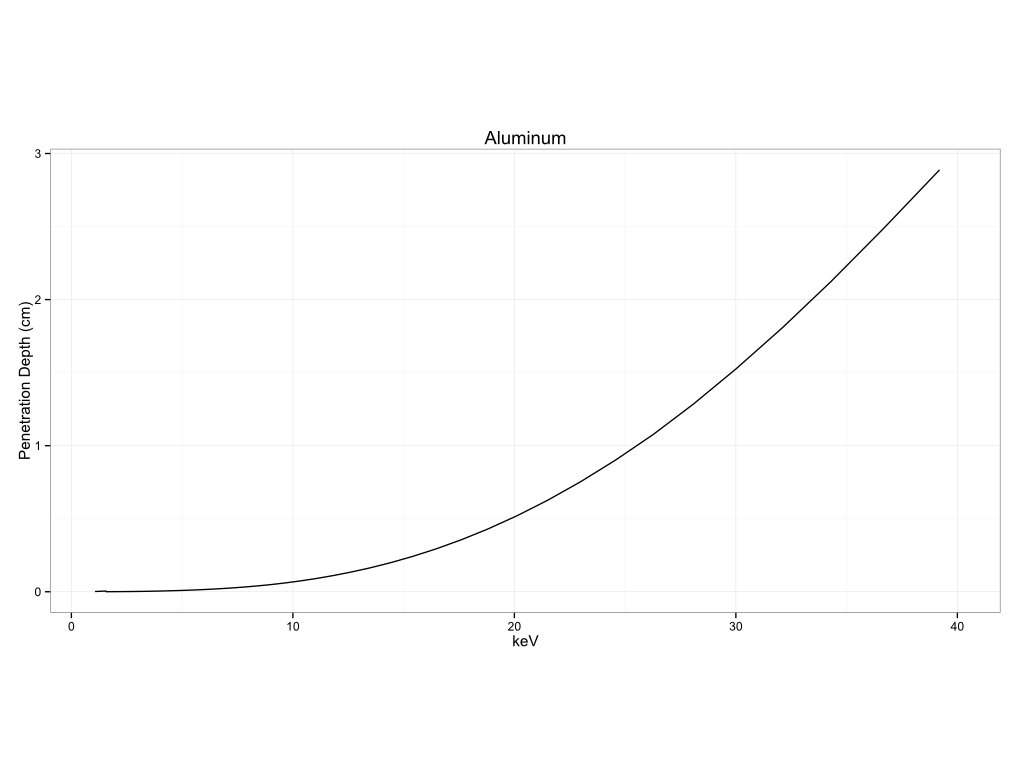
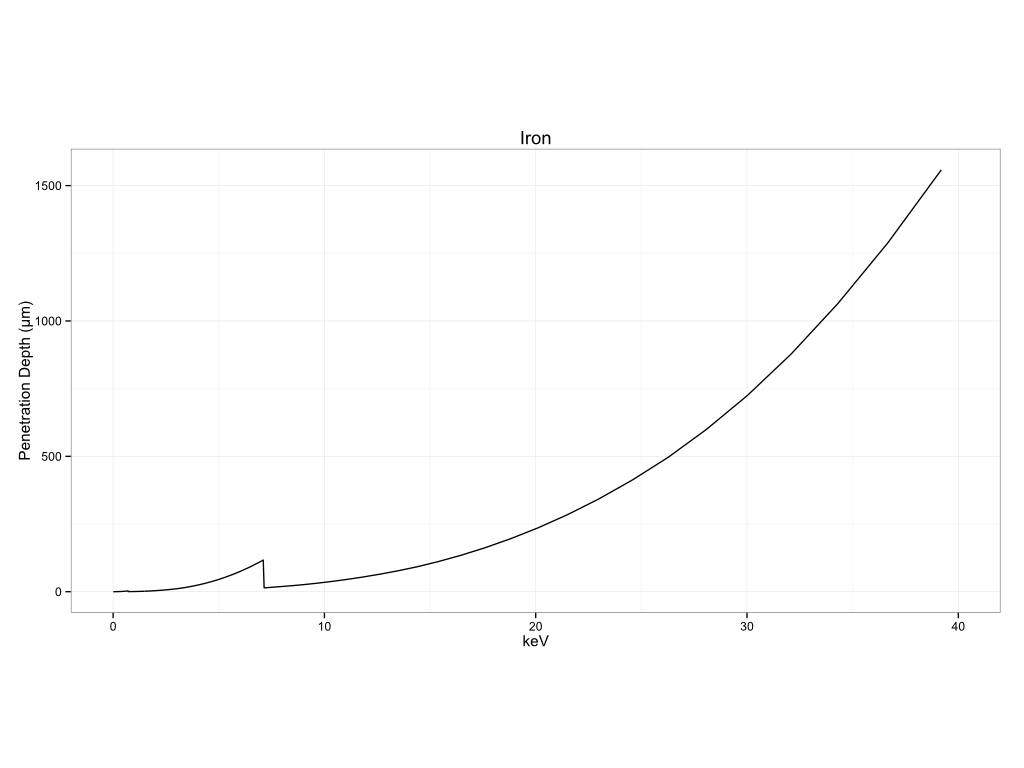
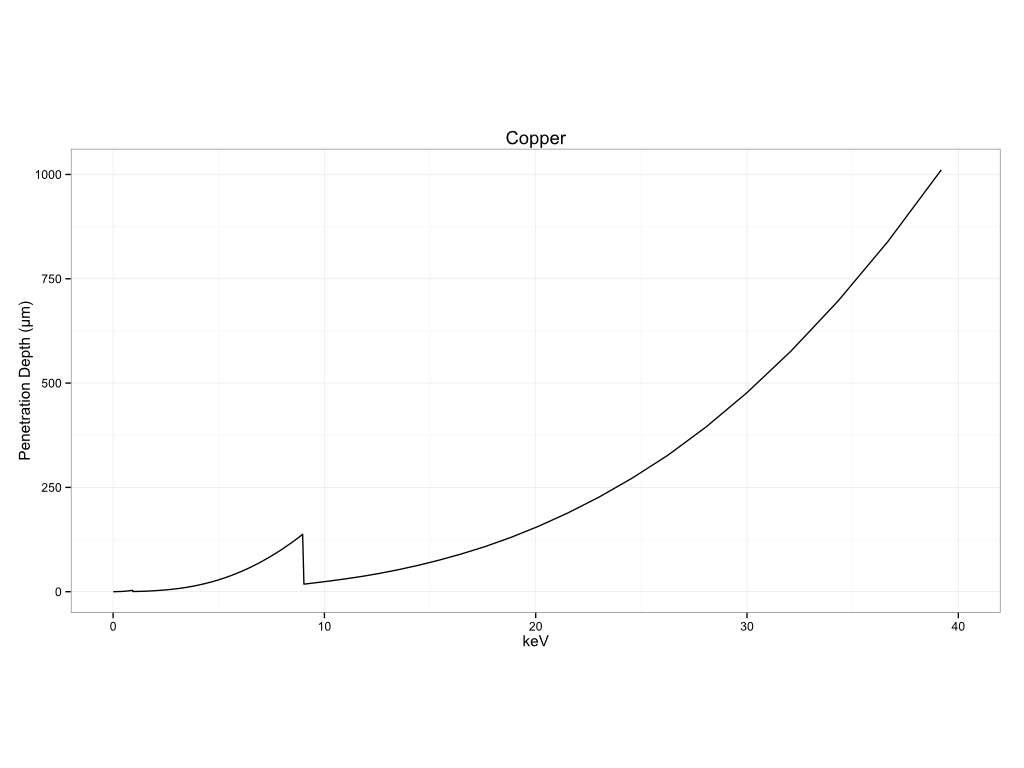
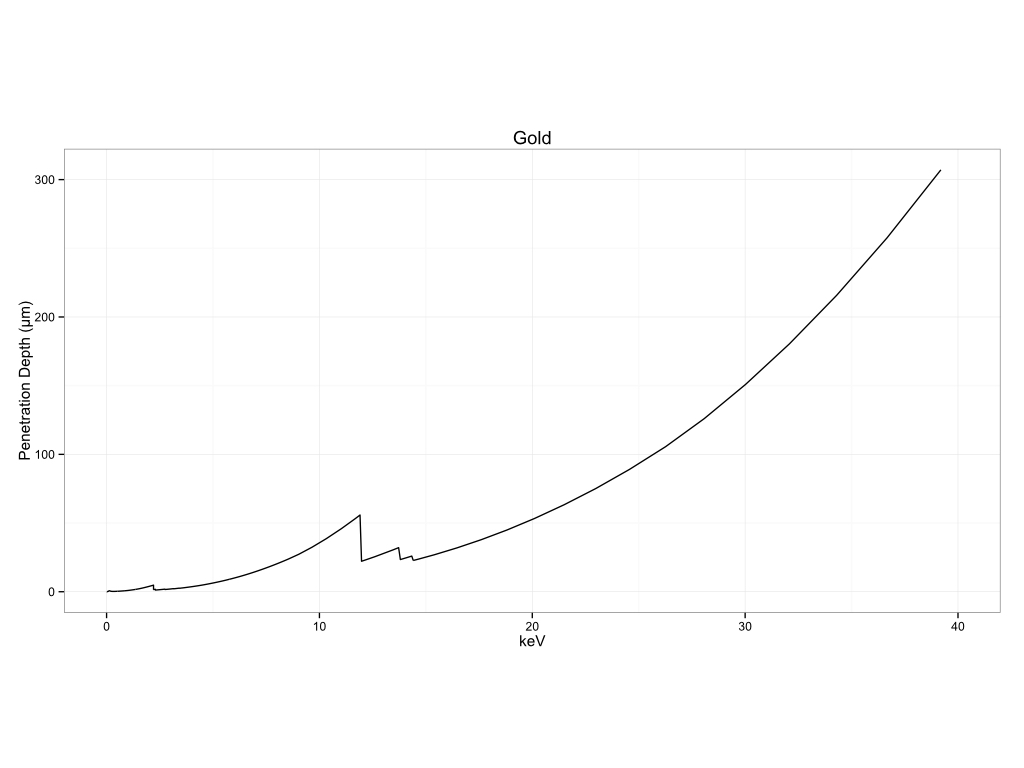
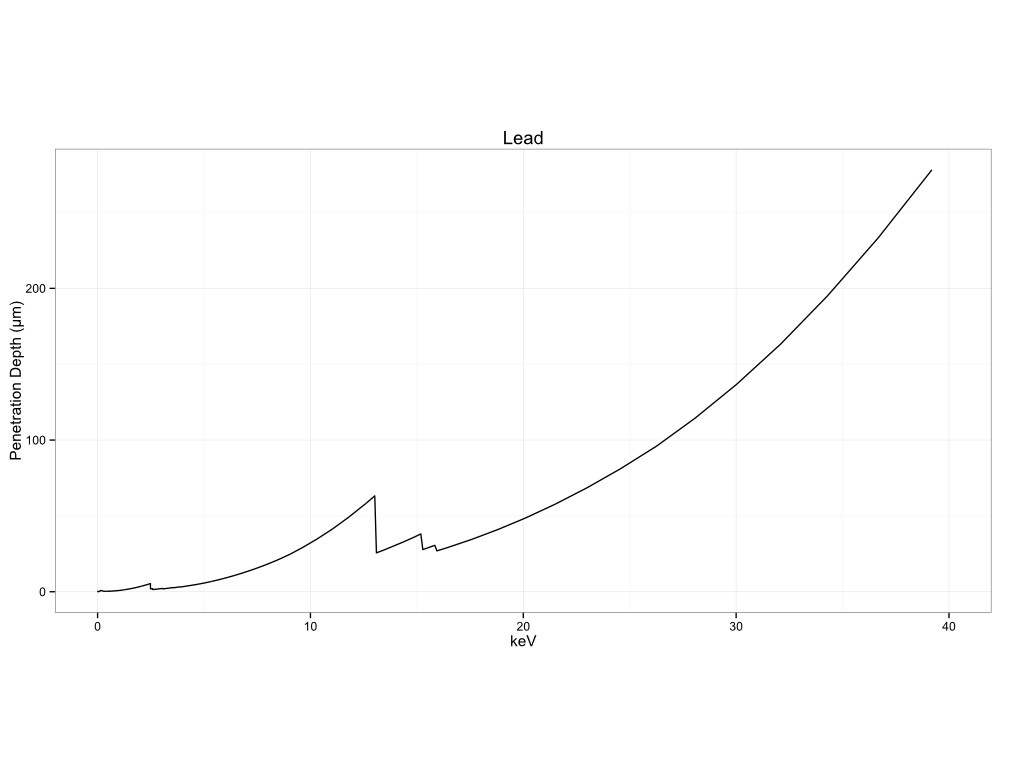
Historical Pigments
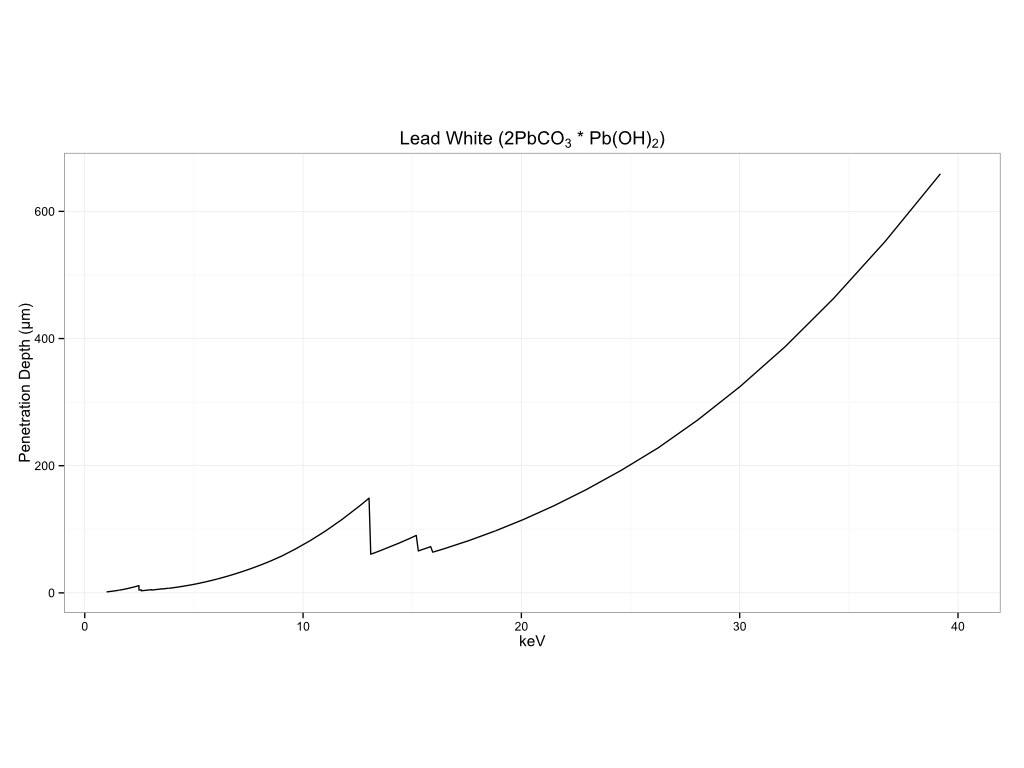
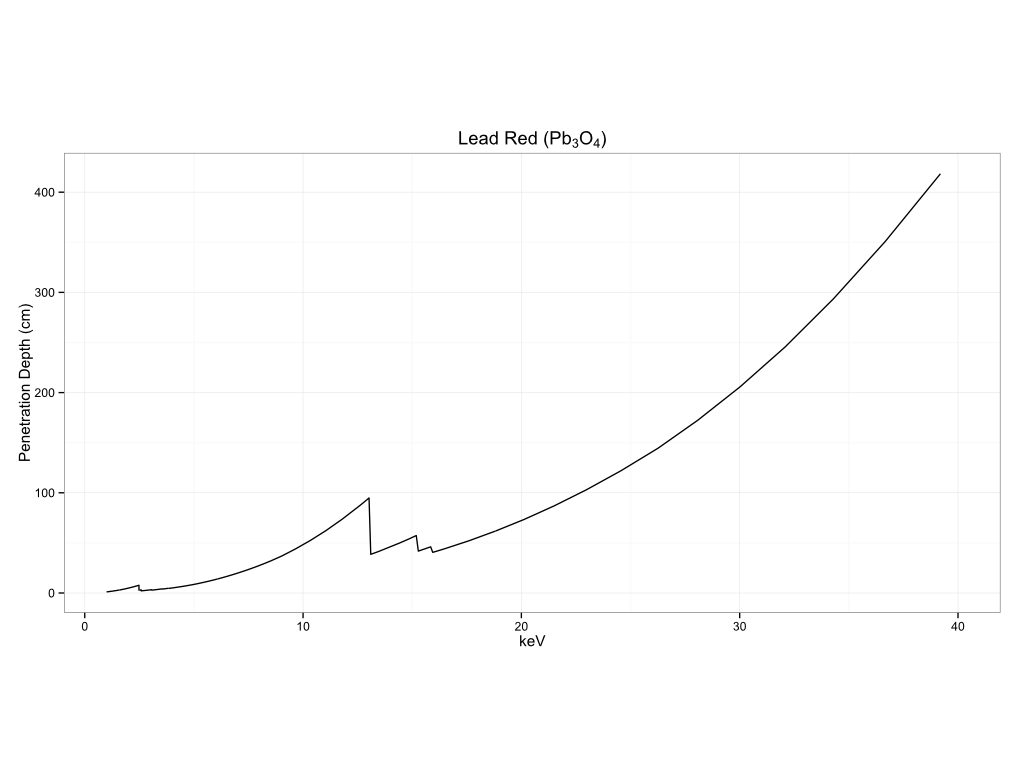
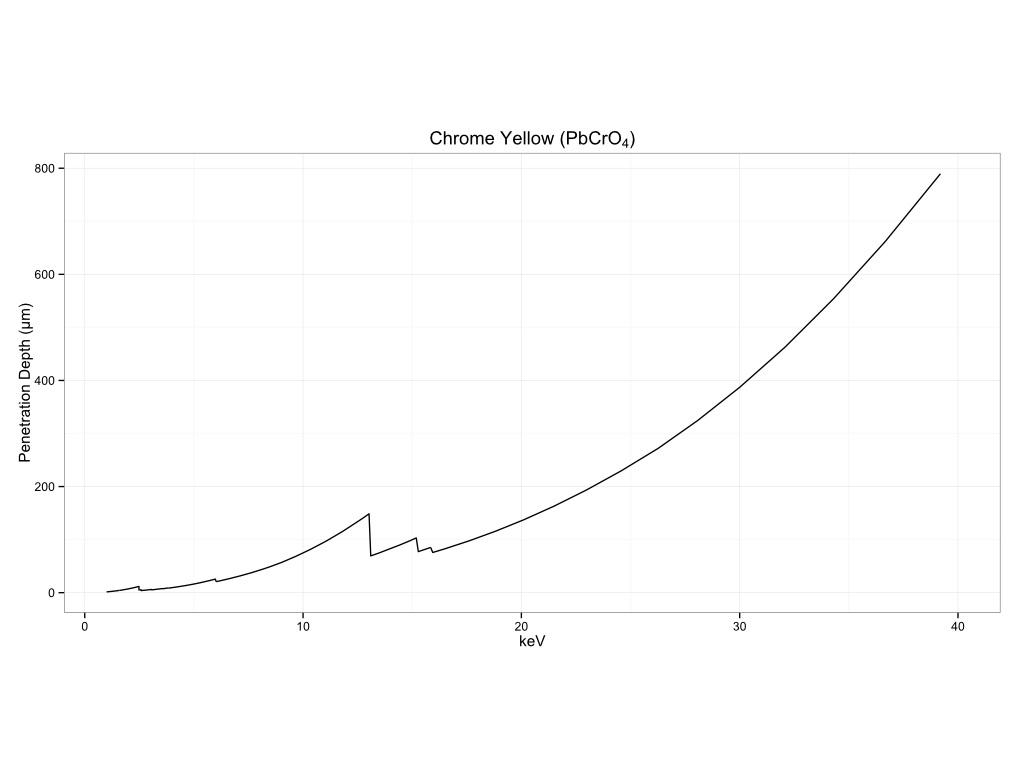
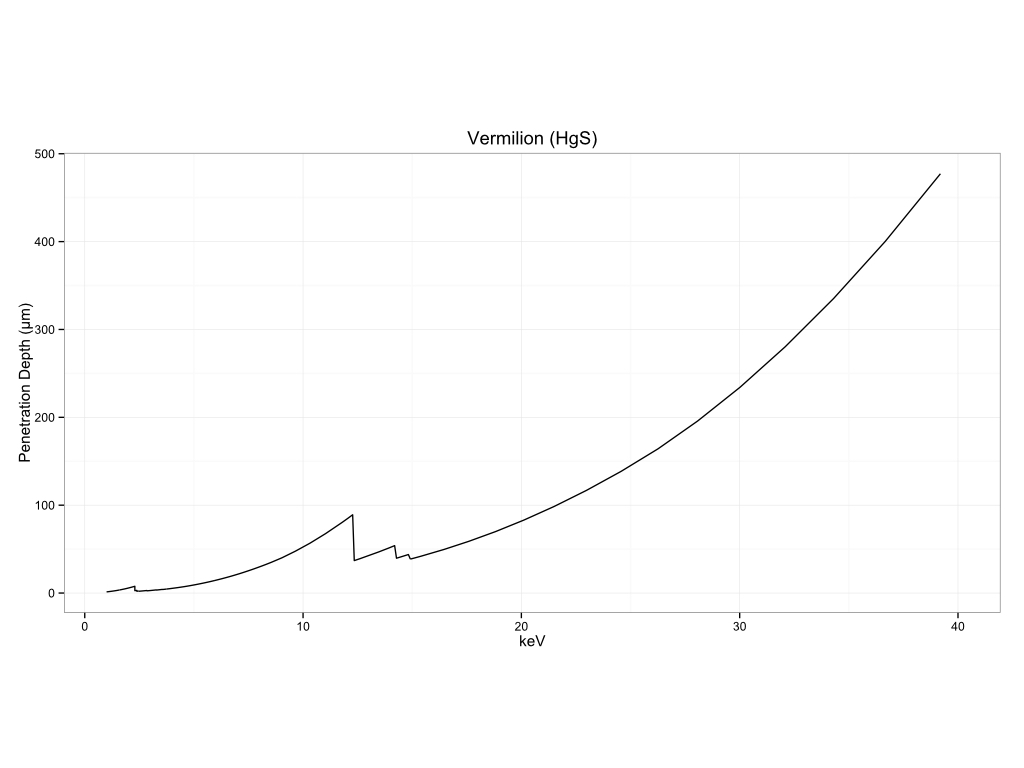
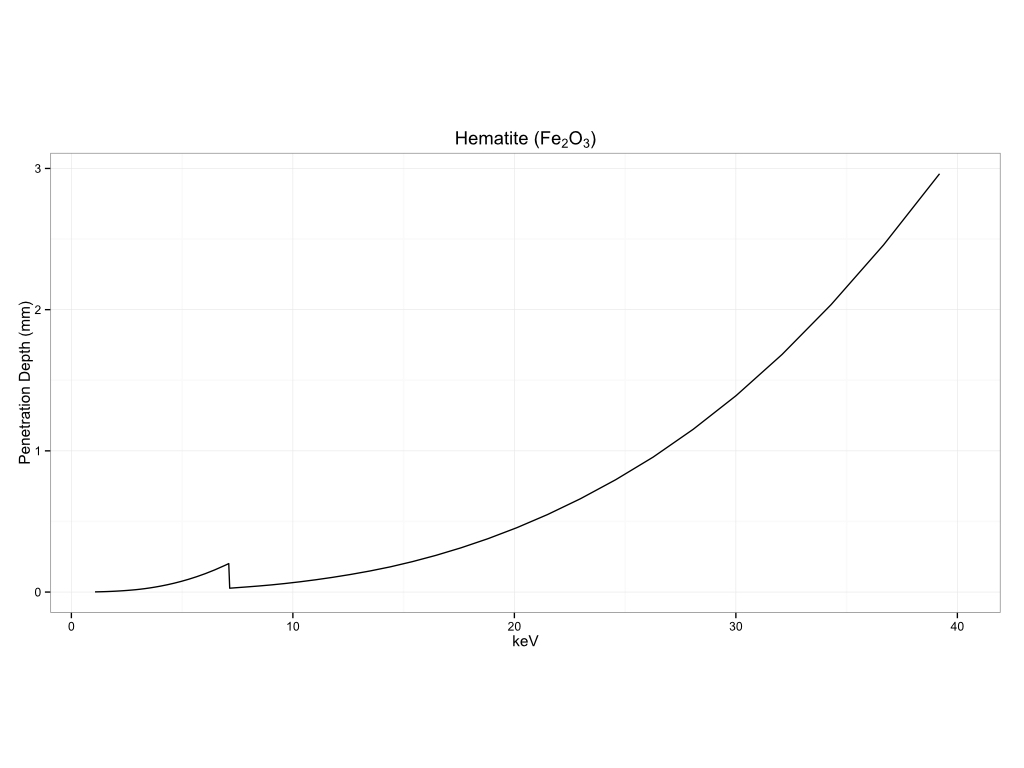
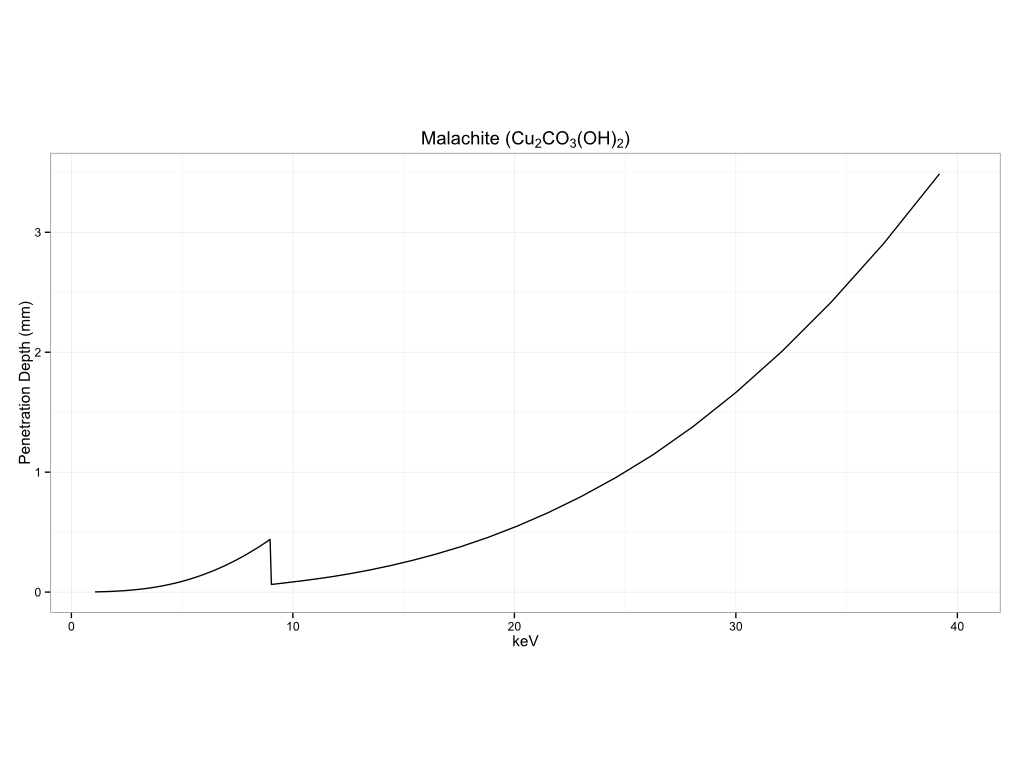
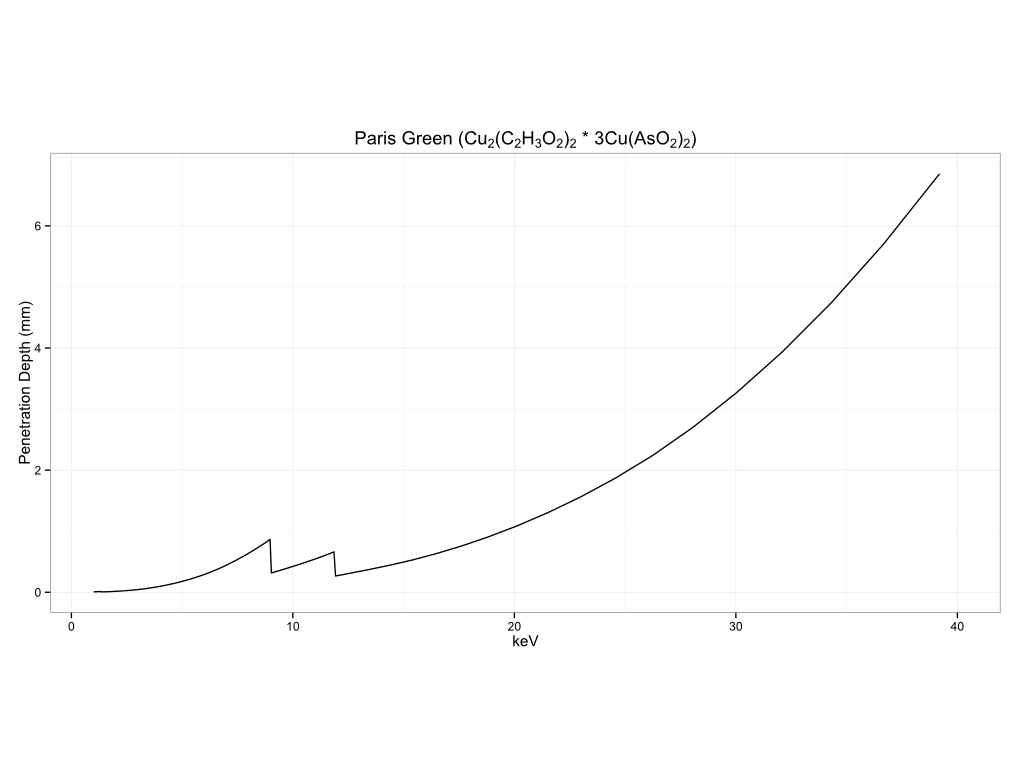
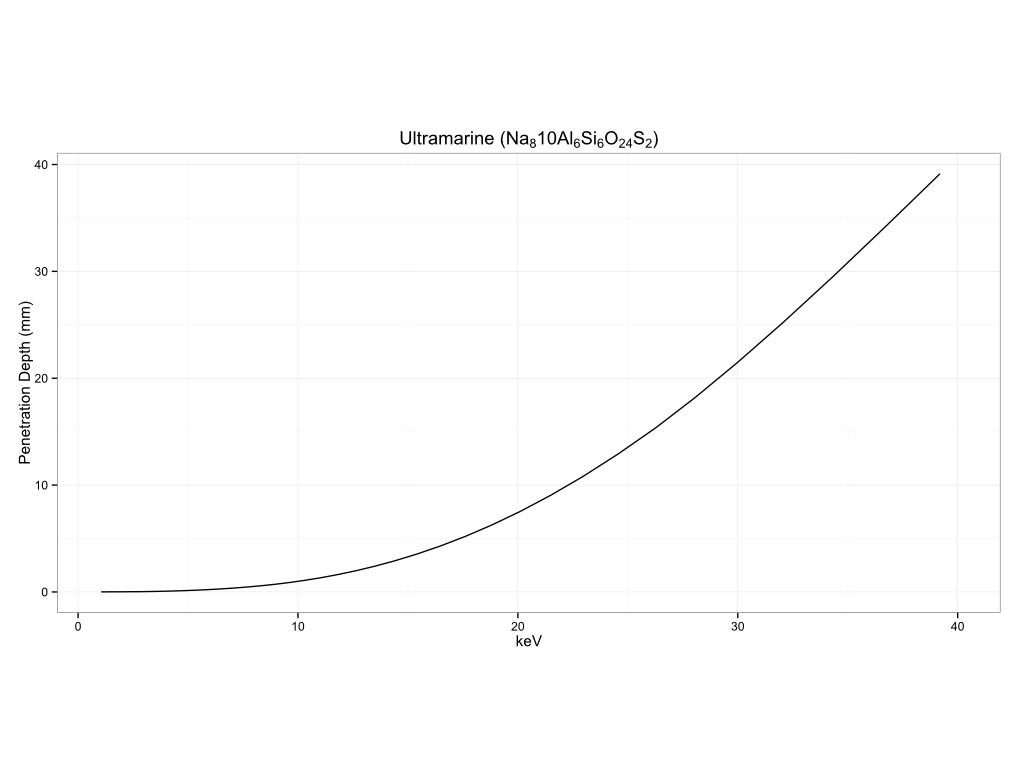
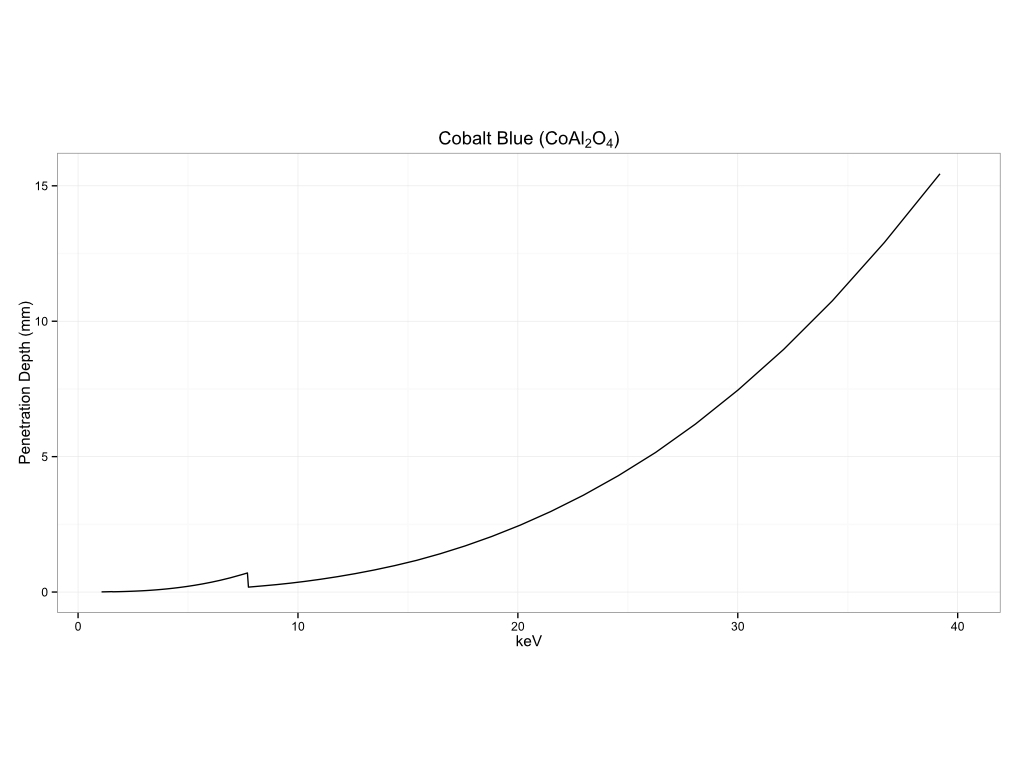
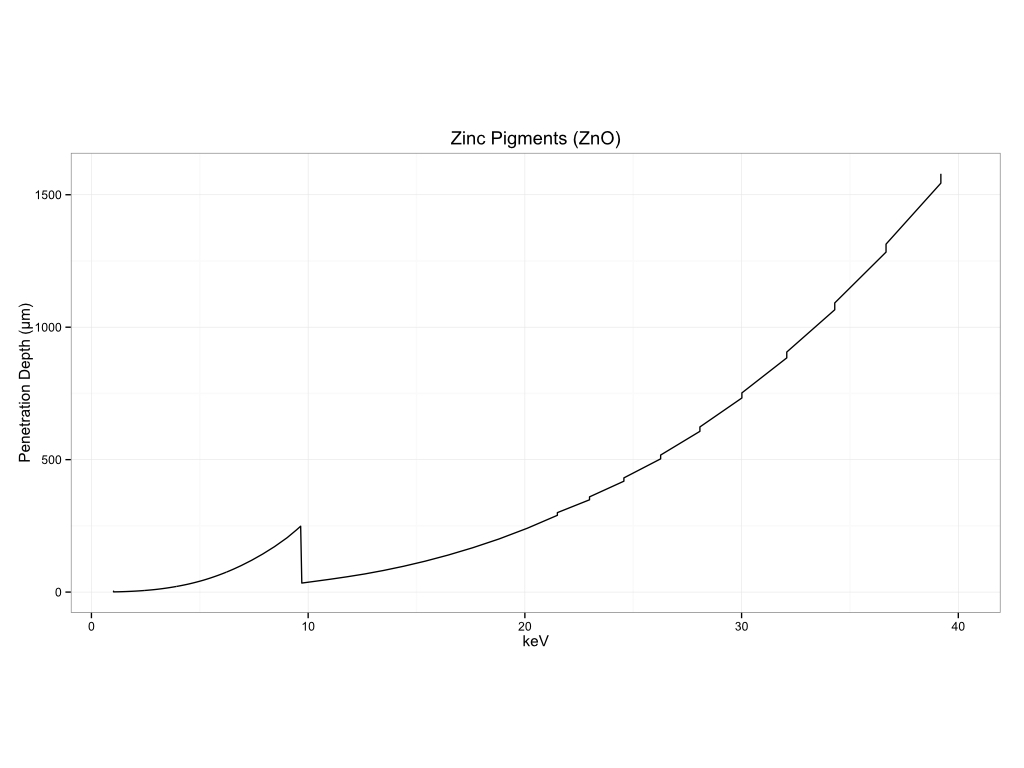
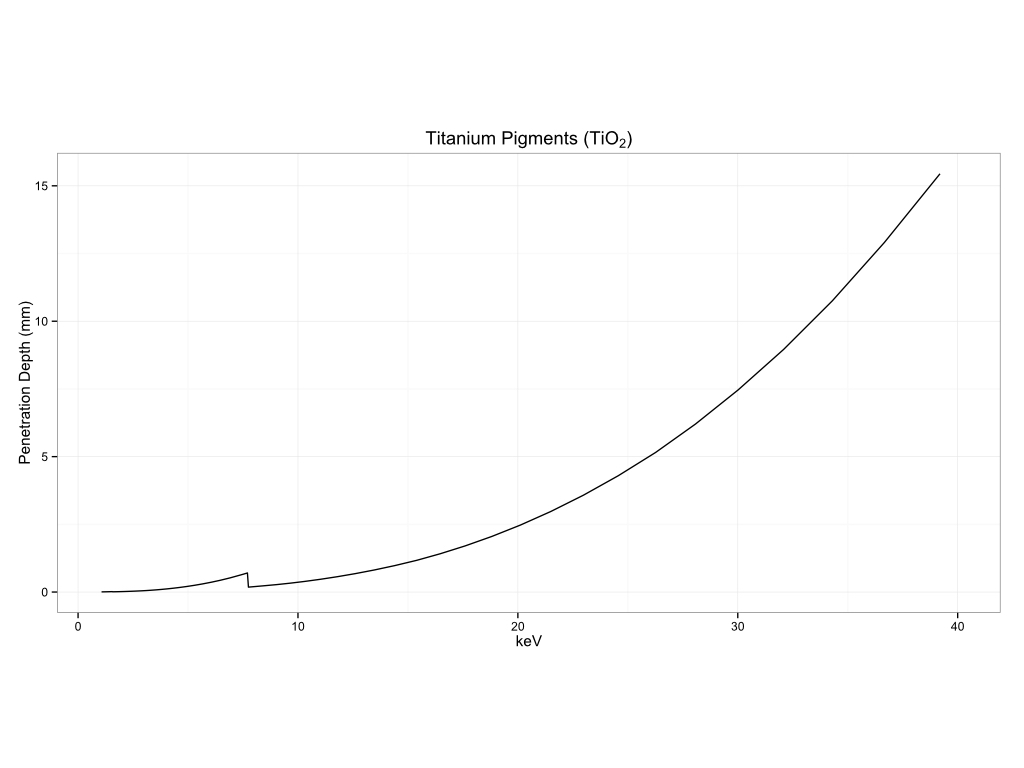
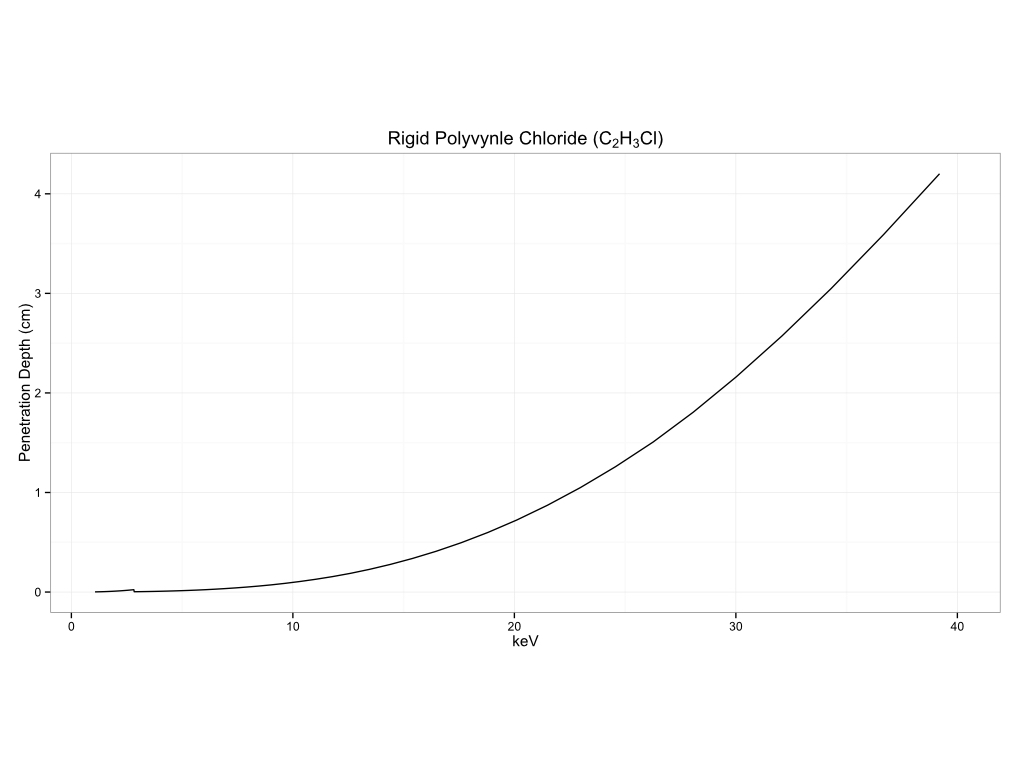
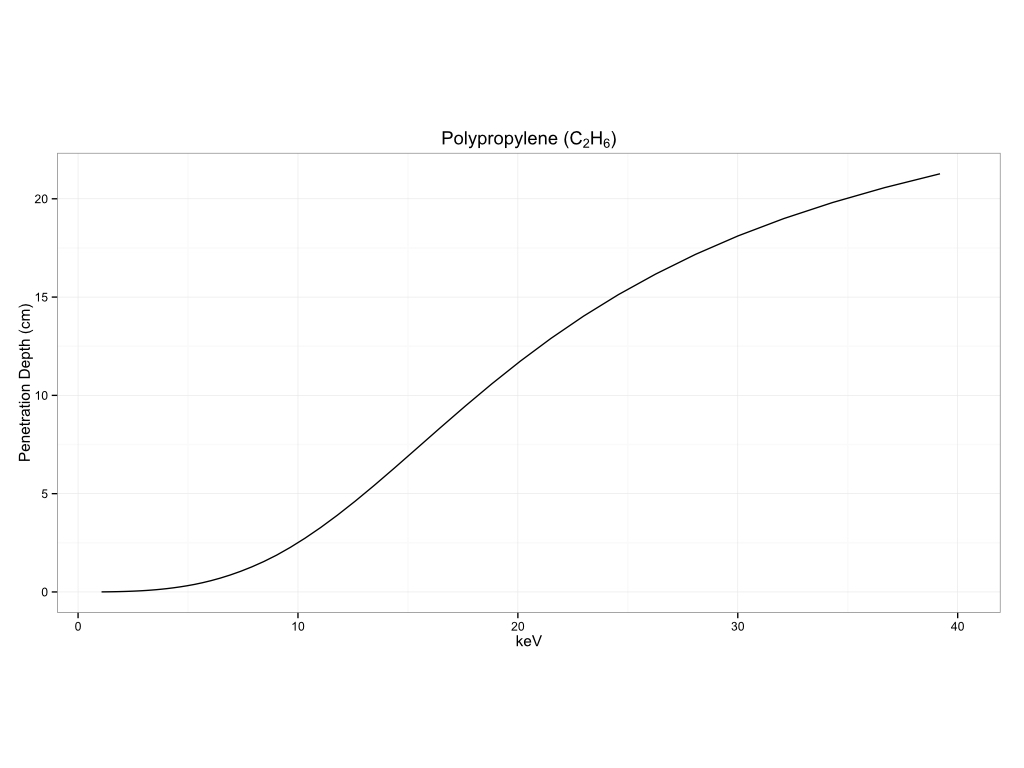
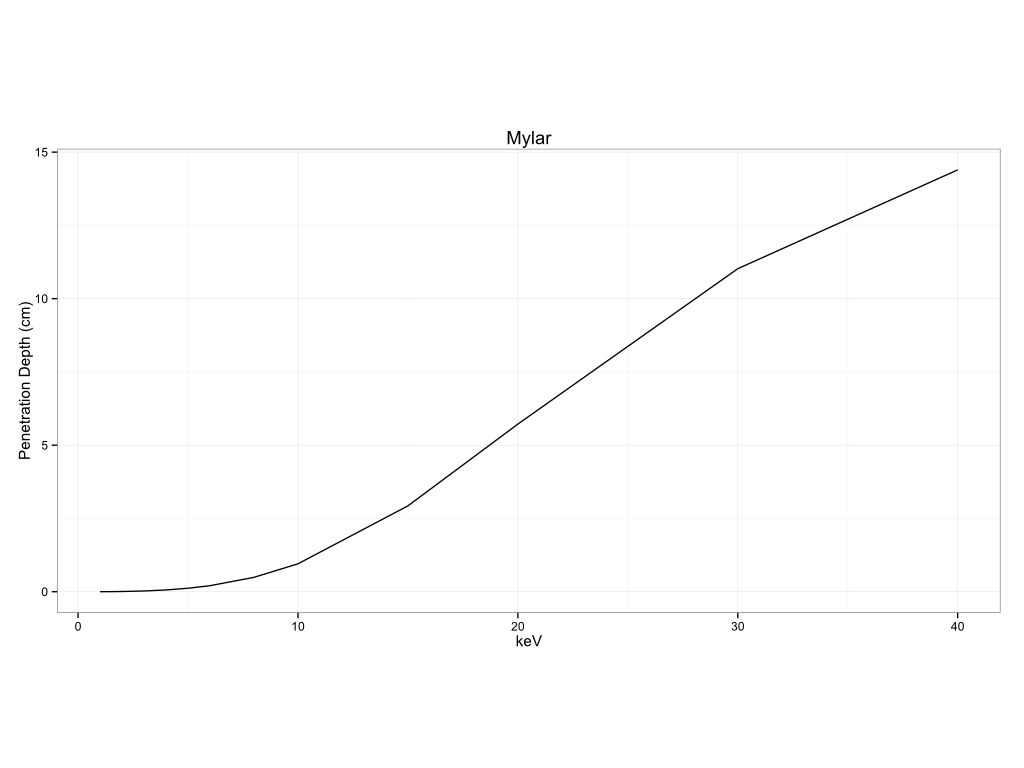
Plastics
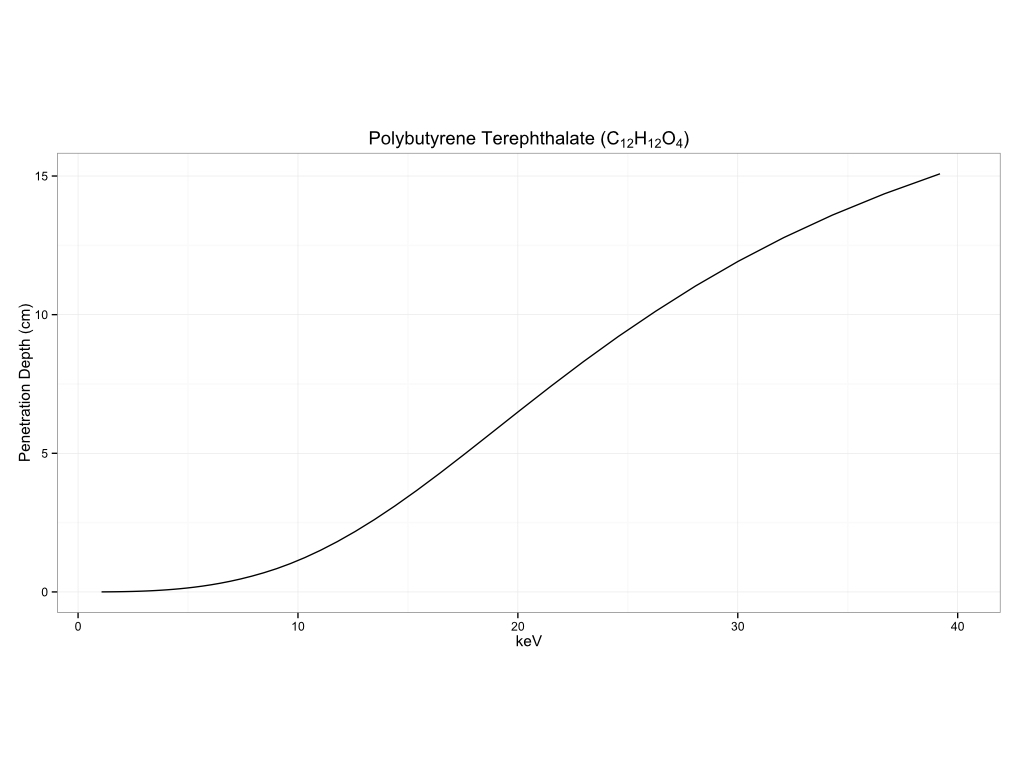
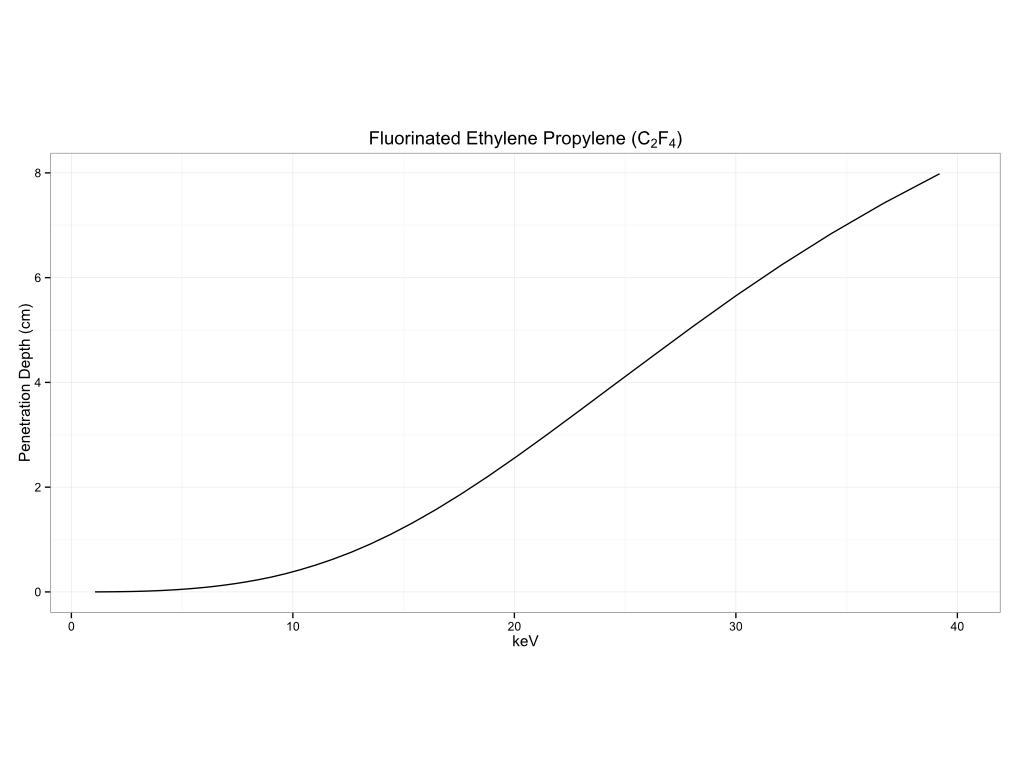
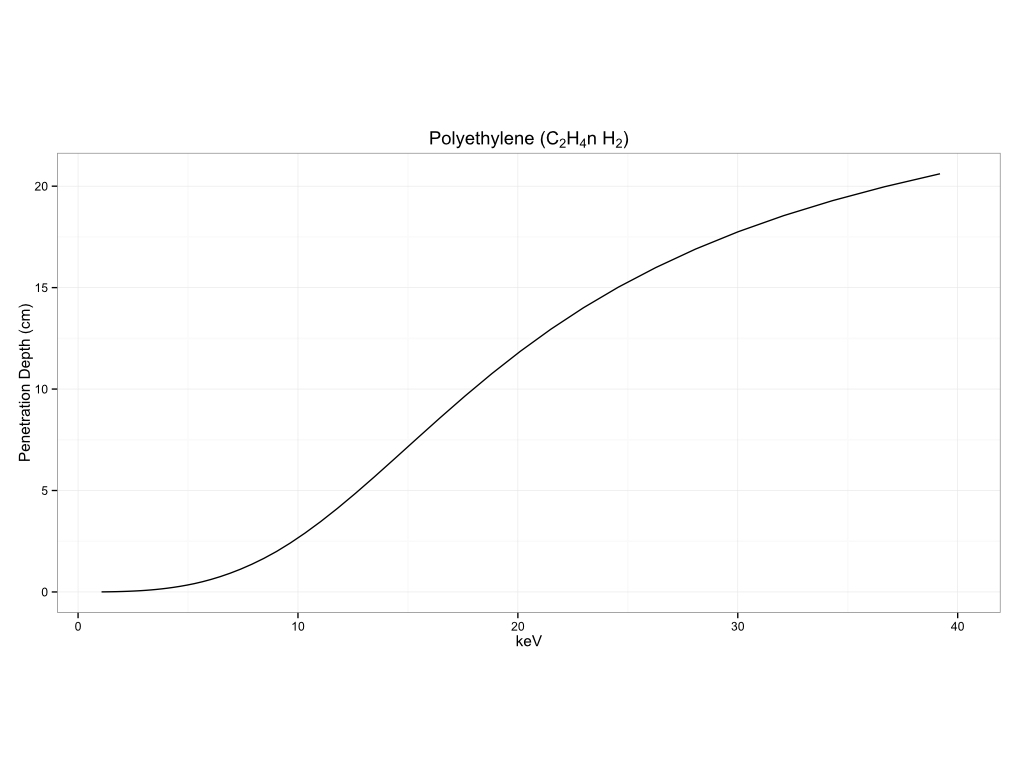
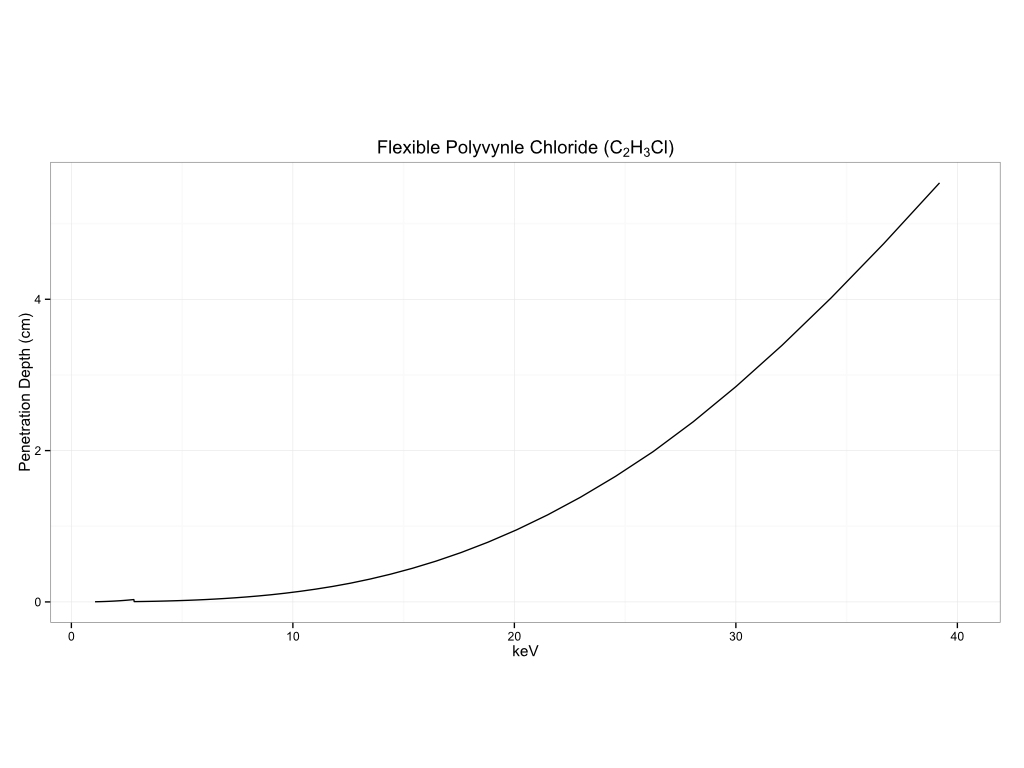
Biological Materials